Trên hệ trục ~Oxy~, cho biểu diễn hình ảnh con đường từ trái qua phải, độ cao của mặt đường tại một điểm có thể là một trong hai trường hợp sau:

• (a) Không thay đổi so với điểm phía trước.
• (b) Độ cao tăng lên hoặc giảm xuống ~1~ đơn vị so với điểm phía trước.

Một chiếc xe di chuyển trên đường từ trái qua phải. Thời gian để xe di chuyển qua một đơn vị độ dài là ~A~ giây đối với trường hợp (a), là ~B~ giây đối với trường hợp (b).

Chúng ta có thể xây dựng một đường hầm dưới núi hoặc một cái cầu cạn bắc ngang qua thung lũng. Đường hầm hoặc cầu phải nằm ngang, nghĩa là phải song song với trục ~Ox~. Thời gian để xe di chuyển qua một đơn vị độ dài trên cầu hoặc trong đường hầm là ~C~ giây.

Yêu cầu

Cho biết độ cao của mặt đường, hãy tìm cách xây dựng đường hầm và cầu sao cho thời gian xe di chuyển hết con đường là nhỏ nhất. Biết rằng tổng số đường hầm và cầu được xây dựng tối đa là ~ K ~.

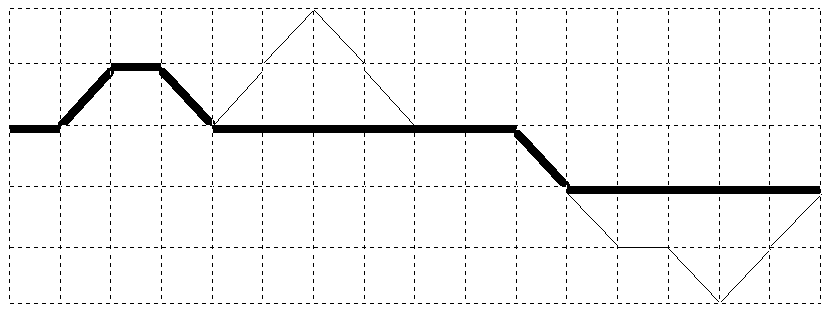
Hình trên mô tả ví dụ bên dưới. Con đường ban đầu biểu diễn bằng nét nhạt, con đường sau khi xây dựng đường hầm và cầu cạn biểu diễn bằng nét đậm. Vì ~K = 2~ , đã xây dựng ~1~ đường hầm và ~1~ cầu cạn nên không thể xây dựng được đường hầm qua ngọn núi đầu tiên.

Dữ liệu vào

Dòng thứ nhất chứa ba số nguyên ~ A, B~ và ~C~ ~(1 \leq A, B, C \leq 100)~.

Dòng thứ hai chứa hai số nguyên ~N~ và ~K~ ~(1 \leq N \leq 30000, 1 \leq K \leq 1000).~

Dòng thứ ~3~ chứa xâu gồm ~N~ kí tự mô tả độ cao mặt đường từ trái qua phải. Mỗi kí tự trong xâu thể hiện một trong các ý nghĩa sau:

• R: Không thay đổi.
• D: Giảm ~1~ đơn vị.
• G: Tăng ~1~ đơn vị.

Các số trên cùng một dòng được ghi cách nhau ít nhất một dấu cách.

Dữ liệu ra

Một số nguyên duy nhất là thời gian nhỏ nhất để xe di chuyển hết con đường theo phương án xây dựng đường hầm và cầu cạn tối ưu.

Sample Input

10 20 15
16 2
RGRDGGDDRRDDRDGG

Sample Output

235