Nhận xét

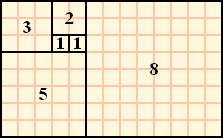
• Tấm ảnh thứ nhất ta nhận được là tấm ảnh ~1 \cdot 1~ có chiều rộng là ~1~.
• Tấm ảnh thứ hai ta nhận được là tấm ảnh ~1 \cdot 2~ có chiều rộng là ~1~.
• Tấm ảnh thứ ba ta nhận được là tấm ảnh ~2 \cdot 3~ có chiều rộng là ~2~.
• Tấm ảnh thứ tư ta nhận được là tấm ảnh ~3 \cdot 5~ có chiều rộng là ~3~.
• Tấm ảnh thứ năm ta nhận được là tấm ảnh ~5 \cdot 8~ có chiều rộng là ~5~.
• Tấm ảnh thứ sáu ta nhận được là tấm ảnh ~8 \cdot 13~ có chiều rộng là ~8~.

Như vậy ta sẽ có dãy fibonacci : ~1,1,2,3,5,8,13,21,34,55,\dots~. Và dãy này mang tính chất:lẻ, lẻ, chẵn, lẻ, lẻ, chẵn, lẻ, lẻ, chẵn, lẻ, lẻ, chẵn, ~\dots ~ .

• Từ cả hai dữ kiện trên ta suy ra:
  • Nếu kết quả ở vị trí lẻ thứ ~N~ thì nó sẽ là vị trí ~\frac{(3 \cdot N+1)}{2} -1~ trong dãy.
  • Nếu kết quả ở vị trí chẵn thứ ~N~ thì nó sẽ là vị trí ~3 \cdot N ~ trong dãy.

Với ~N \le 10^8~ (20 tests)

• Ta áp dụng tính chất trên và dùng mảng đồng thời chia dư để tìm kết quả.

Code tham khảo của lds

void input()
{
    cin>>k>>n;
    if(k==0)
        n=(3*n+1)/2-1;
    else
        n=n*3;
}

int dp[100000000];
void lds_go_goooo()
{
    dp[0]=0;
    dp[1]=1;
    FOR(i,2,n)
        dp[i]=(dp[i-1]+dp[i-2])%mod;
    cout<<dp[n];
}

Độ phức tạp: ~\mathcal{O} (T \cdot N)~. Ta có thể giải bằng cách tạo mảng fibonacci sẵn với độ phức tạp là ~\mathcal{O} (N+T)~

Lưu ý: Ta không thể đếm các phần tử chẵn lẻ của mảng fibonacci để chọn kết quả vì phép ~mod~ cho số lẻ không giữ tính chẵn lẻ.

Với ~N \le 10^{12}~ (10 tests)

• Ta dùng Nhân ma trận để tìm số fibonacci thứ ~N~ trong khoảng ~\mathcal{O} (2^3 \cdot \log{N})~, áp dụng với các tính chất trên ta có code sau.

Code tham khảo của haruxne

#include <bits/stdc++.h>
#define FOR(i,k,n) for(int i = k; i <= n; i++)
#define int long long
using namespace std;

const int MT = 27022007;

struct Matrix{
    int val[3][3];
    Matrix(){
        memset(val,0,sizeof val);
    }
    Matrix operator * (Matrix b){
        Matrix c;
        FOR(i,1,2) FOR(j,1,2) FOR(k,1,2) c.val[i][j] += val[i][k] * b.val[k][j], c.val[i][j] %= MT;
        return c;
    }
    Matrix Pow(int n){
        if (n == 1) return *this;
        Matrix tmp = Pow(n >> 1);
        tmp = tmp*tmp;
        if (n % 2) tmp = tmp * *this;
        return tmp;
    }
};

void solve(){
    int k, n; cin >> k >> n;
    n = (!k) ? (n*3 + 1) /2 -1 : n*3 ;
    Matrix pnlp;
    pnlp.val[1][1] = pnlp.val[1][2] = pnlp.val[2][1] = 1;
    if(n==1)
    {
        cout << pnlp.val[1][1]<< '\n';
        return ;
    }
    pnlp = pnlp.Pow(n-1);
    cout << pnlp.val[1][1] << '\n';
}

signed main(){
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
    int t=1; cin >> t;
    while (t--) solve();
}
//flex

Độ phức tạp: ~\mathcal{O} (T \cdot 2^3 \cdot \log{N})~

Giải thích

Ta có công thức quy hoạch động ~f_i=f_{i-1}+f_{i-2}~

Và trường hợp cơ sở ~f_0=0, f_1=1~

Có:

• ~f_i=1 \cdot f_{i-1}+1 \cdot f_{i-2}~
• ~f_{i-1}=1 \cdot f_{i-1}+0 \cdot f_{i-2}~

Vì thế ta có ma trận ban đầu:

~A=\begin{bmatrix} 1 & 1\\ 1 & 0\\ \end{bmatrix}~

Và kết quả bài toán là:

~\begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix}^{N-1} \cdot \begin{bmatrix} 1\\ 0\\ \end{bmatrix} = \begin{bmatrix} f_N\\ f_{N-1}\\ \end{bmatrix} ~

Có điều đó là do:

~\begin{bmatrix} f_N\\f_{N-1}\end{bmatrix} =A \cdot \begin{bmatrix} f_{N-1}\\f_{N-2}\end{bmatrix} = A^2 \cdot \begin{bmatrix} f_{N-2}\\f_{N-3}\end{bmatrix}=A^3 \cdot \begin{bmatrix} f_{N-3}\\f_{N-4}\end{bmatrix}=\dots=A^{N-1} \cdot \begin{bmatrix} f_1\\f_0\end{bmatrix} ~ .