Một dự án xây dựng trường học gồm hai tòa nhà. Trên bảng vẽ, nhìn từ trên xuống các tòa nhà có thể xem như các hình chữ nhật có cạnh song song với hệ trục tọa độ và không giao nhau. Mỗi hình chữ nhật được xác định bởi tọa độ góc trái dưới và phải trên. Hình thứ nhất có tọa độ góc trái dưới ~(x_1,y_1)~ và phải trên ~(x_2, y_2)~. Hình thứ hai có tọa độ góc trái dưới ~(x_3,y_3)~ và phải trên ~(x_4,y_4)~. Tọa độ đều là các số nguyên có giá trị tuyệt đối không vượt quá ~10^6~.

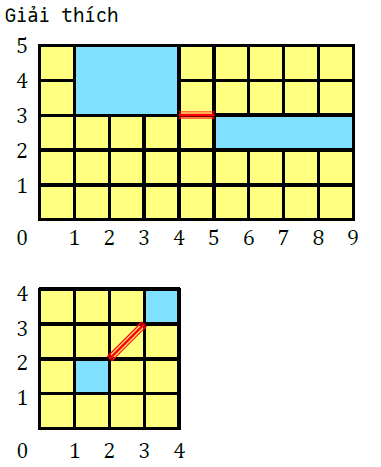
Để tiện lại cho việc đi lại giữa hai tòa nhà và tránh mưa nắng, người ta muốn làm một đường đi bộ có mái che nối hai tòa nhà. Trên bản vẽ, đường mái che là một đoạn thẳng nối một điểm trên cạnh hình chữ nhật này đến một điểm trên cạnh của hình chữ nhật còn lại. Để tiết kiệm chi phí, người ta cần tìm phương án làm đường mái che sao cho độ dài của của đoạn thẳng tương ứng là nhỏ nhất có thể.

Yêu cầu:

Cho trước ~8~ giá trị ~x_1,y_1,x_2,y_2,x_3,y_3,x_4~ và ~y_4~. Hãy tính bình phương độ dài ngắn nhất của đoạn cần làm mái che.

Dữ liệu:

• Dòng ~1~ chứa số nguyên dương ~T ≤ 10^4~ là số test
• ~T~ dòng tiếp theo, mỗi dòng chứa ~8~ số nguyên ~x_1,y_1,x_2,y_2,x_3,y_3,x_4~ và ~y_4~ có giá trị tuyệt đối không quá ~10^6~ ứng với một test

Kết quả:

Ứng với mỗi test, ghi ra bình phương độ dài đoạn mái che tìm được trên một dòng

Sample Input

2
1 3 4 5 5 2 9 3
1 1 2 2 3 3 4 4

Sample Output

1
2

Nguồn: thầy Lê Minh Hoàng