Cuộc thi chạy bộ Marathon năm 2020 của thành phố RACE sẽ được tổ chức trong mạng giao thông của thành phố. Mạng gồm có ~N~ nút giao thông đánh số từ ~1~ đến ~N~, được nối với nhau bởi ~N-1~ đoạn đường. Mỗi đoạn đường nối hai nút giao thông phân biệt đều cho phép đi theo cả hai chiều và có độ dài đo bằng kí-lô-mét là số nguyên. Giữa hai nút giao thông bất kỳ có đúng một đường đi từ nút này đến nút kia qua dãy các đoạn đường nối tiếp nhau mà không qua bất cứ nút giao thông nào quá một lần. Ban tổ chức cuộc thi tiến hành khảo sát mạng giao thông nói trên và cần tìm ra đường đua cho cuộc thi thỏa các yêu cầu sau:

• Đường đua có thể bắt đầu từ một nút giao thông bất kỳ và kết thúc tại một nút bất kỳ (khác nút xuất phát) miễn sao đường đua phải dài đúng ~K~ kí-lô-mét;
• Không có đoạn đường nào được sử dụng quá một lần trên đường đua;
• Để hạn chế ảnh hưởng đến giao thông, đường đua phải chứa một số ít nhất các đoạn đường nếu có thể.

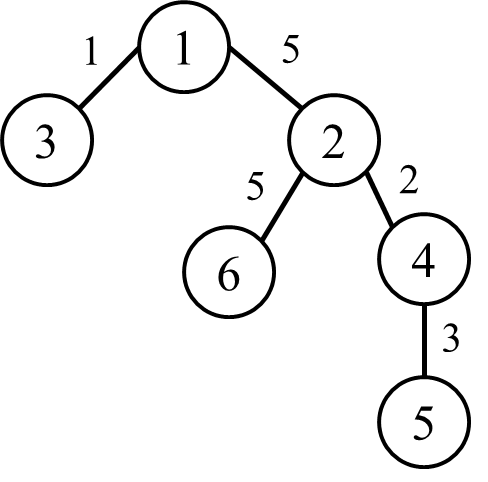
Ví dụ, trong hình minh họa nêu trên, giả sử độ dài đường đua là ~10~ kí-lô-mét, ta có thể tìm được ~3~ đường đua là:

• Đường đua ~(1): 1 – 2 – 6~
• Đường đua ~(2): 1 – 2 – 4 – 5~
• Đường đua ~(3): 6 – 2 – 4 – 5~
  Do đường đua số ~(1)~ có số đoạn đường ít nhất (bằng ~2~) nên đường đua này sẽ được chọn để thi đấu.

Yêu cầu:

Hãy giúp ban tổ chức tìm đường đua thỏa mãn các yêu cầu đặt ra.

Dữ liệu:

• Dòng đầu chứa hai số ~N~ và ~K (1 \leq N \leq 500, 1 \leq K \leq 10^4)~;
• Trong ~N-1~ dòng tiếp theo, mỗi dòng ghi ba số ~i, j, C_{ij} ~là số hiệu hai nút giao thông ~i, j~ và độ dài đoạn đường nối chúng ~(1 \leq Cij \leq 10^3)~. Các số trên cùng dòng viết cách nhau một dấu cách.

Kết quả:

Gồm một số duy nhất là số lượng đoạn đường ít nhất thuộc đường đua được ban tổ chức chọn thi đấu. Nếu không tìm được đường đua thỏa yêu cầu thì ghi số ~-1~.

Sample Input

6 10
1 2 5
1 3 1
2 4 2
2 6 5
4 5 3

Sample Output

2