An có niềm đam mê với lý thuyết đồ thị và cô ấy chỉ vừa mới học về cây khung nhỏ nhất. An có ba số nguyên ~n~, ~m~, ~s~ và cần dùng chúng để dựng một đồ thị có tính chất sau:

• Đồ thị có ~n~ đỉnh và ~m~ cạnh vô hướng trong đó mỗi cạnh có độ dài là một số nguyên dương.
• Không có cạnh nào kết nối một đỉnh với chính nó và mỗi cặp đỉnh có nhiều nhất một cạnh nối.
• Đồ thị là đồ thị liên thông, một đỉnh có thể đi tới bất kỳ đỉnh nào khác.
• Giá trị của cây khung nhỏ nhất là ~s~, có nghĩa là tổng độ dài của tất cả các cạnh của cây khung nhỏ nhất thuộc đồ thị là ~s~.
• Tổng độ dài của tất cả các cạnh thuộc đồ thị là nhỏ nhất.

Ví dụ, với ~n=4, m=5~ và ~s=4~. Chúng ta cần dựng một đồ thị với ~4~ đỉnh, ~5~ cạnh và giá trị của cây khung nhỏ nhất là ~4~ như hình bên dưới.

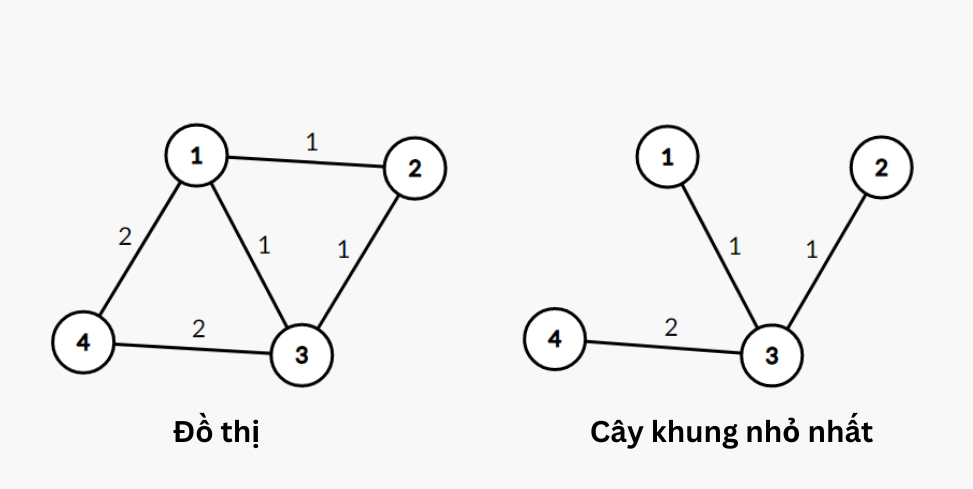
Độ dài của tất cả các cạnh thuộc đồ thị trên là ~7~.

Cho ~n, m~ và ~s~, hãy tìm tổng độ dài nhỏ nhất của tất cả các cạnh thuộc đồ thị thỏa mãn yêu cầu trên.

Lưu ý: Dữ liệu vào đảm bảo với mọi bộ ba số ~n, m, s~ được cho thì ta đều có thể tạo một đồ thị hợp lệ.

Input

• Dòng đầu tiên chứa một số nguyên ~T~, số lượng đồ thị.
• Mỗi dòng của ~T~ dòng tiếp theo chứa 3 số nguyên ~n, m, s~.

Output

• Gồm ~T~ dòng, mỗi dòng in ra một số nguyên là tổng độ dài nhỏ nhất của tất cả các cạnh thuộc đồ thị thỏa mãn yêu cầu tương ứng.

Scoring

• Subtask ~1~ (20%):
  • ~1\le g\le 100~
  • ~2\le n\le 10~
  • ~1\le m\le 50~
  • ~1\le s\le 20~
• Subtask ~2~ (30%):
  • ~1\le g\le 100~
  • ~2\le n\le 50~
  • ~1\le m\le 2000~
  • ~1\le s\le 200~
• Subtask ~3~ (20%):
  • ~1\le g\le 100~
  • ~2\le n\le 10^5~
  • ~1\le m\le 10^{10}~
  • ~1\le s\le 10^6~
• Subtask ~4~ (30%):
  • ~1\le g\le 1000~
  • ~2\le n\le 10^8~
  • ~1\le m\le 10^{16}~
  • ~1\le s\le 10^{10}~

Sample Input

2
4 5 4
4 3 6

Sample Output

7
6

Note

• Testcase ~1~: Đáp án đã được giải thích ở phần ví dụ phía trên.
• Testcase ~2~: Ta cần dựng một đồ thị với ~4~ đỉnh, ~3~ cạnh và giá trị cây khung nhỏ nhất là ~6~. Một đồ thị liên thông gồm ~n~ đỉnh và ~n-1~ cạnh chính là một cây, vì vậy cây khung nhỏ nhất sẽ chính là đồ thị ban đầu và tổng độ dài tất cả các cạnh thuộc đồ thị sẽ bằng với giá trị cây khung nhỏ nhất. Vì vậy đáp án là ~6~.