Nhà máy V đang thử nghiệm ~\pi-robot~ trên một lưới ô vuông khổng lồ. Một số ô là điểm sạc (chứa ổ cắm điện). Robot lúc đầu đứng ở một ô. Sau khi vận hành, robot sẽ đi qua một số ô, ở mỗi ô một số nguyên dương phút, rồi sau đó sẽ di chuyển sang ô hàng xóm kề cạnh (thời gian di chuyển là không đáng kể). Hãy xác định giá trị lớn nhất có thể của khoảng cách bé nhất từ Robot đến một điểm sạc nào đó sau khi robot vận hành ~N~ phút. Khoảng cách được sử dụng là khoảng cách Manhattan.

Khoảng cách Manhattan giữa hai ô có tọa độ (~x, y~) và (~u, v~) là ~\left | x-y \right | + \left | u-v \right |~

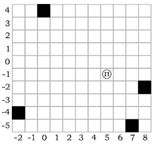
Trong ví dụ trên ~4~ điểm sạc là các ô màu đen, robot ban đầu ở ô có vòng trắng. Sau ~5~ phút, robot có thể đến ô (~2, -1~) và lúc này khoảng cách gần nhất đến một điểm sạc là ~7~. Và đó là giá trị lớn nhất.

Dữ liệu vào

Dòng đầu ghi số điểm sạc ~U~ (~1 \leq U \leq 10^4~) và số phút thử nghiệm ~N~ (~1 \leq N \leq 10^9~). Sau đó là ~U~ dòng, mỗi dòng ghi ~2~ số nguyên là tọa độ một điểm sạc (~x, y~). Dòng cuối ghi tọa độ lúc ban đầu của robot. Các tọa độ thỏa mãn ~-10^9 \leq x, y \leq 10^9~. Toàn bộ ~U+1~ điểm đôi một phân biệt.

Kết quả ra

In ra giá trị lớn nhất của khoảng cách bé nhất từ robot đến một điểm sạc.

Giới hạn

~25\%~ số test có ~ N \leq 300~.

~35\%~ số test có ~N > 300~ và các tọa độ thỏa mãn ~0 \leq |x|, |y| \leq 10^3~

~40\%~ số test không có giới hạn gì thêm.

Sample Input

4 5 
0 4 
-2 -4 
8 -2 
7 -5 
5 -1

Sample Output

7

Nguồn: PreVOI 2019