1. Đệ quy

Trong cuộc sống, chúng ta thường thấy hình ảnh về những vật mà bên trong lại chứa một vật khác giống hệt nó, như hình ảnh trong sách giáo khoa Toán lớp 3 cũ, màn hình của streamer khi họ mở cửa sổ ứng dụng live stream, link này, ... Trong khoa học máy tính, ta gọi đó là đệ quy. Trong bài viết này, chúng mình sẽ giúp các bạn hiểu rõ hơn về đệ quy và cách ứng dụng nó trong tin học.

1.1 Khái niệm

Ta gọi một đối tượng là đệ quy (recursion) nếu nó được định nghĩa qua chính nó hoặc một đối tượng cùng dạng với chính nó bằng quy nạp.

Ví dụ:

• Tìm số fibonacci thứ $n$, ta có $fib(n) = fib(n - 1) + fib(n - 2)$

Nếu một bài toán $P$ có lời giải được thực hiện bằng bài toán con $P'$ có dạng giống $P$ thì đó là một giải thuật đệ quy. $P'$ ở đây là một bài toán đơn giản hơn $P$ và không cần đến $P$ để giải nó.

Khi bài toán $P'$ đã tối giản, không thể thực hiện bài toán con đơn giản hơn nữa mà phải có lời giải riêng cho trường hợp này thì ta gọi đó là trường hợp cơ sở.

Ta cũng có thể gọi một hàm là đệ quy nếu hàm đó tự gọi chính nó.

1.2 Cài đặt

Đề bài: cho số tự nhiên $n$ $(n \le 50)$. Hãy tìm số fibonacci thứ $n$.

Cài đặt cơ bản

Nhận xét

Dựa vào tính chất đã nêu trên để xét, ta cần có trường hợp cơ sở là $fib(1)$ và $fib(2)$ (tùy tài liệu). Ở bài viết này chúng mình sẽ chọn $fib(1) = 0$ và $fib(2) = 1$

Code mẫu

long long fib(int n) {
    if (n == 1) return 0;
    if (n == 2) return 1;
    long long fib1 = 0, fib2 = 1, ans;
    for (int i = 3; i <= n; i++) {
        ans = fib1 + fib2;
        fib1 = fib2;
        fib2 = ans;
    }
    return ans;
}

Đây là một cách khá tốt để giải bài toán này, tuy nhiên ở bài viết này ta đang tìm hiểu về đệ quy, nên ta cũng có thể dùng đệ quy để giải quyết bài toán một cách ngắn gọn hơn.

Cài đặt bằng đệ quy

Để hiểu cách mà đệ quy hoạt động, trước hết hãy xem xét trường hợp $n = 4$, để tính $fib(4)$, ta phải tính qua $fib(2)$ và $fib(3)$, để tính $fib(3)$, ta phải tính qua $fib(2)$ và $fib(1)$, để tính $fib(2)$, ta có $2$ lựa chọn sau:

• Tính qua $fib(0)$ và $fib(1)$
• Thay $fib(2) = 1$, $fib(1) = 0$ vào và tính tiếp.

Lựa chọn thứ nhất có vẻ không khả thi, phần vì ta chưa quy ước $fib(0)$ là bao nhiêu, phần vì cứ tiếp tục thì ta sẽ chẳng biết phải dừng ở đâu cả. Vậy khi thay $fib(1) = 0, fib(2) = 1$ ta đã có thể tính tiếp được $fib(3)$, có $fib(2)$ và $fib(3)$, ta có thể tính tiếp được $fib(4)$.

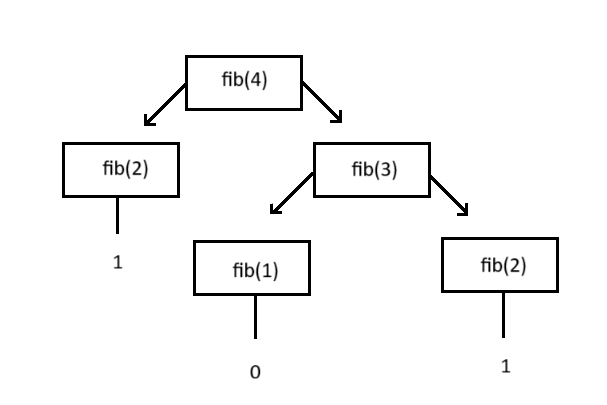
Phân tích dài dòng nhưng code lại khá đơn giản.

Code mẫu

long long fib(int n) {
    if (n == 1) return 0;           // nếu đang xét đến số fibonacci thứ 1
    if (n == 2) return 1;           // hoặc 2 thì trả về 0 hoặc 1
    return fib(n - 2) + fib(n - 1); // nếu không thì trả về tổng số thứ n - 2 và n - 1
}

1.3 Ứng dụng

Ưu điểm mà chúng ta thấy ngay được của việc sử dụng đệ quy là viết code ngắn gọn hơn. Ở một số bài toán lớn, việc không sử dụng đệ quy sẽ làm bài giải của chúng ta cồng kềnh hơn rất nhiều, ví dụ khi duyệt cây và đồ thị.

Nhược điểm dễ thấy là khi không tính toán độ phức tạp hoặc không sử dụng các kỹ thuật lưu trữ dữ liệu, giải bằng đệ quy đôi khi sẽ tốn thời gian chạy và bộ nhớ vô cùng lớn!

Ngoài ra ta còn dùng đệ quy cho hầu hết các bài toán sử dụng giải thuật quay lui dưới đây.

2. Quay lui

2.1 Khái niệm

Thuật toán quay lui (backtracking) dùng để giải bài toán liệt kê các cấu hình. Mỗi cấu hình được xây dựng bằng cách xây dựng từng phần tử, mỗi phần tử được chọn bằng cách thử tất cả các khả năng.

Việc thử hết toàn bộ khả năng khiến cho giải thuật này còn có tên gọi khác là vét cạn.

2.2 Cài đặt

Một hàm quay lui thông thường có cấu trúc như sau:

void backtrack(int pos) {   
    // Trường hợp cơ sở
    if (<pos là vị trí cuối cùng>) {
        <lưu lại tập hợp đã dựng nếu thoả mãn>
        return;
    }

    //Phần đệ quy
    for (<tất cả giá trị i có thể ở vị trí pos>){
        <thêm giá trị i vào tập đanh xét>
        backtrack(pos + 1);
        <xoá bỏ giá trị i khỏi tập đang xét>
    }
}

Việc thêm giá trị mới vào tập đang xét rồi cuối cùng xoá bỏ nó ra khỏi tập giải thích cho tên gọi "quay lui" của thuật toán. Đó là việc khôi phục lại trạng thái cũ của tập hợp sau khi kết thúc việc gọi đệ quy.

Cụ thể hơn, ta hãy làm một bài tập kinh điển về quay lui.

Đề bài: cho số tự nhiên $n$ $(n \le 20)$. Hãy sinh tất cả xâu nhị phân có độ dài $n$. Ví dụ: với $n = 3$, ta có danh sách các xâu nhị phân $000,001,010,011,100,101,110,111$.

Cách giải bài này theo tư tưởng quay lui như sau: ta xây dựng từng ký tự cho từng xâu trong danh sách. Ở ký tự tiếp theo, ta sử dụng xâu đã xây dựng trước đó và tiếp tục chọn. Bạn đọc có thể xem ảnh dưới để hiểu một cách trực quan cho trường hợp $n = 3$

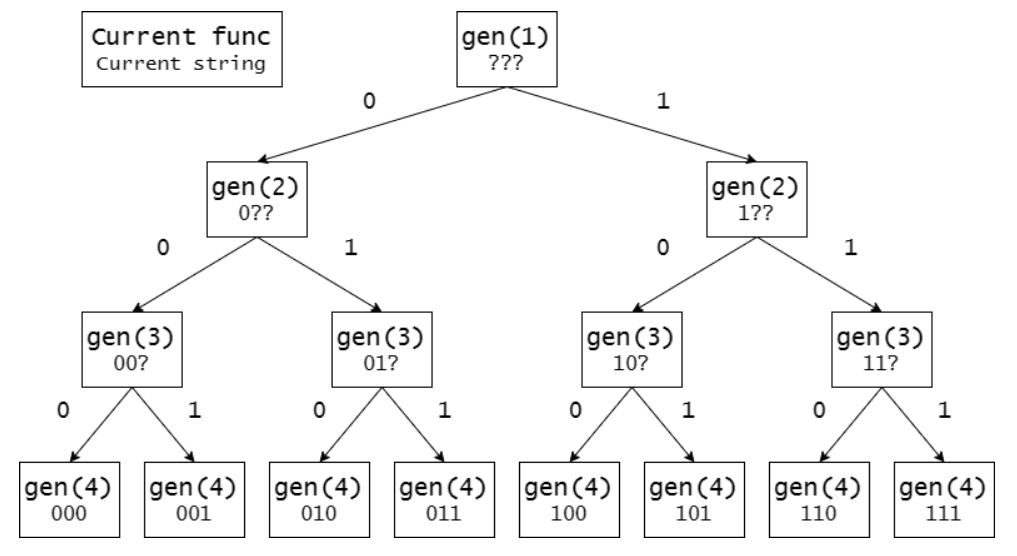
Code tham khảo

int n;
string cur;

void gen(int i) {
    if (i > n) {                        // xâu đã xây dựng xong
        cout << cur << '\n';
        return;
    }
    for (char c = '0'; c <= '1'; c++) { // chọn từng trường hợp khi xây dựng
        cur.push_back(c);
        gen(i + 1);                     // với trường hợp đã chọn, xây dựng ký tự tiếp theo
        cur.pop_back();                 // bỏ ký tự này đi
    }
}

int main() {
    cin >> n;
    cur = "";
    gen(1);
    return 0;
}

Ta cũng có thể giải bài này mà không cần dùng đệ quy bằng cách sử dụng các thao tác trên bit. Phần này chúng mình nhường bạn đọc tìm hiểu.

Đề bài: cho $n$ quả táo $(n \le 20)$, quả thứ $i$ có khối lượng là $a_i$. Hãy tìm cách chia số quả táo này vào $2$ tập sao cho chênh lệch khối lượng là nhỏ nhất.

Ý tưởng: Với quả táo thứ $i$, ta thử thêm nó vào tập $1$ hoặc tập $2$ và xét đến quả táo tiếp theo. Khi đã đủ $n$ quả táo, ta tính độ chênh lệch và lấy $min$.

Code tham khảo

int n;
vector <int> weights;

int recurse_apples(int index, int sum1, int sum2) {                      // Khi đã đủ n quả táo
    if (index == n) { 
        return abs(sum1 - sum2);
    }
    return min(recurse_apples(index + 1, sum1 + weights[index], sum2),   // thêm vào tập 1
           recurse_apples(index + 1, sum1, sum2 + weights[index]));  // thêm vào tập 2
}

int main() {
    cin >> n;
    weights.resize(n);
    for (int i = 0; i < n; i++) cin >> weights[i];

    // Bắt đầu với 0 quả táo ở cả 2 tập
    cout << recurse_apples(0, 0, 0);
    return 0;
}

2.3 Ứng dụng

Ta dùng quay lui ở những bài toán cần thử toàn bộ khả năng để tìm kết quả tốt nhất. Đây là một cách hiệu quả khi gặp những bài toán có bộ dữ liệu lớn nhưng số trường hợp có thể xảy ra lại nhỏ.

Trong lập trình thi đấu, khi gặp những bài toán phức tạp không thể đưa ngay lời giải tối ưu, ta có thể dùng quay lui để hiểu được bản chất của những trường hợp nhỏ, từ đó xây dựng lời giải cho bài toán tổng quát.

Đây cũng là cách thường dùng để ăn điểm khi không thể tìm được lời giải tổng quát trong những kỳ thi.

3. Bài tập làm thêm

• VNOJ - Tháp Hà Nội 2
• CLAOJ - Số cách
• CLAOJ - Chia nhau mua bánh

4. Nguồn tham khảo

• VNOI - Đệ quy và Thuật toán quay lui
• USACO - Complete Search with Recursion