Sau cuộc gặp gỡ với các em trường Tiểu học và Trung học cơ sở La Ngâu, bé Bi muốn có một đêm liên hoan vui vẻ ấm cúng nên đã chuẩn bị một ít que pháo hoa cầm tay và bóng bay. Tuy nhiên, loại pháo hoa cầm tay mà Bi dùng khá mạnh, có thể làm vỡ bóng bay ngay khi tiếp xúc. Vì vậy Bi đã thử nghiệm để tìm khoảng cách an toàn bằng cách đặt một que pháo sao cho tâm pháo đúng ở vị trí ~A~~(x_A, y_A, z_A)~ và đặt bóng bay ở một khoảng cách nhất định để tính khoảng cách giới hạn từ tâm pháo đến mặt bóng bay.

Vấn đề là Bi đã quên mất vị trí mình đặt bóng bay, chỉ nhớ rằng trong số ~n~ điểm mà Bi đã ghi lại có ~1~ điểm là tâm của quả bóng, và ~n-1~ điểm còn lại đều phân biệt nằm trên mặt bóng. Biết rằng bóng bay của Bi có dạng mặt cầu, bạn hãy giúp Bi tìm khoảng cách từ tâm pháo đến mặt bóng bay mà Bi đã thử nghiệm để chuẩn bị cho một buổi liên hoan hoàn hảo nhé!

Dữ liệu

• Dòng đầu tiên chứa số nguyên ~n~.
• Dòng thứ ~2~ chứa ~3~ số thực là tọa độ của điểm ~A~.
• Trong ~n~ dòng tiếp theo, dòng thứ ~i~ ~(1 \le i \le n)~ chứa ~3~ số thực là tọa độ của điểm thứ ~i~, không có ~4~ điểm bất kì nào cùng nằm trên một mặt phẳng.

Kết quả

• Ghi ra màn hình một số thực duy nhất là kết quả bài toán (làm tròn đến số thập phân thứ ~2~).

Ràng buộc

• ~|x_i|, |y_i|, |z_i| \le 10^3~.
• Có ~50\%~ test có ~5 \le n \le 10^3~.
• Có ~50\%~ test có ~5 \le n \le 10^5~.

Ví dụ

Dữ liệu

5
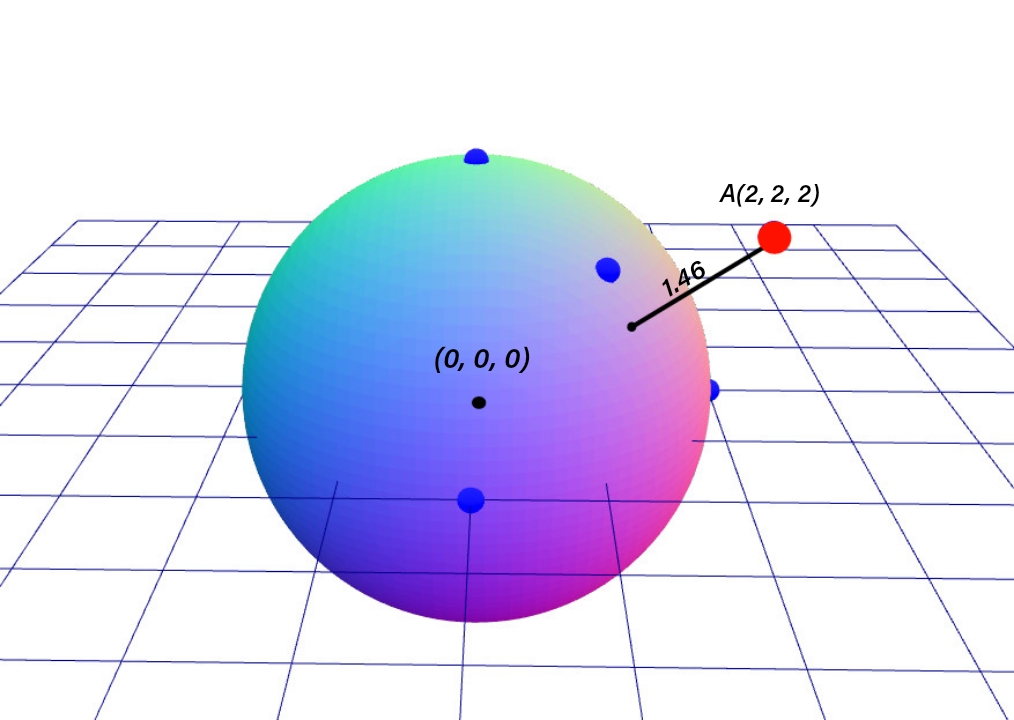
2 2 2
2 0 0
0 0 2
0 2 0
1 1 1.41421
0 0 0

Kết quả

1.46

Giải thích

• Trong test ví dụ trên, điểm ~(0, 0, 0)~ chính là tâm của quả bóng, các điểm còn lại nằm trên mặt bóng